Examples of Mechanism Kinematics#
This document presents a series of examples of kinematic analysis of planar mechanisms.
Example 2.1: Position Analysis of a Four-Bar Linkage#
The figure shows a 4-bar mechanism. At the instant when the crank forms an angle \(\theta_2 = 135^{\circ}\) with the horizontal, calculate the coordinates of point C and the angles that links 3 and 4 form with the horizontal, \(\theta_3\) and \(\theta_4\).
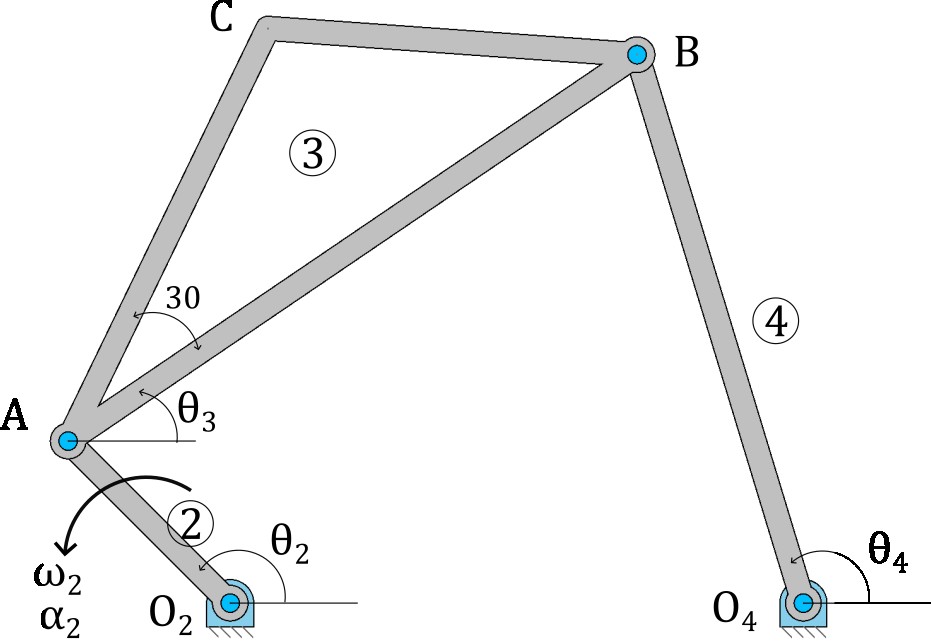
Mechanism Data#
Link lengths, in meters:
\(\overline{O_2A} = 0.2\)
\(\overline{AB} = 0.6\)
\(\overline{O_4B} = 0.5\)
\(\overline{O_2O_4} = 0.5\)
\(\overline{AC} = 0.4\)
Section 1: Position Analysis (Graphical Method)#
The objective is to construct the mechanism’s configuration to scale for the instant \(\theta_2 = 135^\circ\) and measure the requested coordinates and angles.
Construction Data:#
Link 1 (Frame): \(L_1 = \overline{O_2O_4} = 0.5 \text{ m}\)
Link 2 (Crank): \(L_2 = \overline{O_2A} = 0.2 \text{ m}\)
Link 3 (Coupler): \(L_3 = \overline{AB} = 0.6 \text{ m}\)
Link 4 (Rocker): \(L_4 = \overline{O_4B} = 0.5 \text{ m}\)
Point of Interest C: Located on the coupler, with \(\overline{AC} = 0.4 \text{ m}\) and a fixed angle of \(30^\circ\) counter-clockwise with respect to the segment AB.
Construction Procedure:#
Establish the frame (Link 1)
A global coordinate system is defined. The fixed pivot \(O_2\) is located at the origin (0,0).
The second fixed pivot \(O_4\) is located at (0.5, 0), establishing the length and position of the fixed link.
Position the crank (Link 2)
From \(O_2\), link 2 is drawn with its length \(L_2 = 0.2 \text{ m}\) and the input angle \(\theta_2 = 135^\circ\). The end of this vector is the position of joint A.
The coordinates of A can be calculated directly for verification: \(A = (L_2 \cos\theta_2, L_2 \sin\theta_2)\).
Locate joint B (Loop closure)
Coupler Constraint: Point B must be at a distance \(L_3 = 0.6 \text{ m}\) from A. Geometrically, this is a circle with center A and radius 0.6.
Rocker Constraint: Point B must also be at a distance \(L_4 = 0.5 \text{ m}\) from \(O_4\). Geometrically, this is a circle with center \(O_4\) and radius 0.5.
Resolve configuration ambiguity
The intersection of the two circles from the previous step gives two possible solutions for point B. These two solutions define the two configurations (or branches) of the mechanism:
Open Configuration: Generally the one with the larger angle \(\angle O_4BA\) (the “elbow” outwards).
Crossed Configuration: The one with the smaller angle \(\angle O_4BA\) (the “elbow” inwards).
The upper solution for B is chosen, corresponding to the open configuration.
Locate the point of interest C
Point C forms a rigid triangle ABC with the coupler link.
The segment AB is drawn, which defines the orientation of the coupler.
The vector \(\vec{AC}\) is constructed with a magnitude of 0.4 m, rotated \(30^\circ\) counter-clockwise with respect to the direction of the vector \(\vec{AB}\). The end of this vector is point C.
Measurement of results
With the mechanism completely drawn, the desired quantities are measured directly from the graphical software:
Coordinates of point C: \((x_C, y_C)\).
Angle of the coupler, \(\theta_3\): The angle of the segment AB with the horizontal.
Angle of the rocker, \(\theta_4\): The angle of the segment \(O_4B\) with the horizontal.
The following GeoGebra model shows the result of carrying out this process:
Section 2: Position Analysis (Analytical Method)#
The objective is to find expressions for the unknowns (\(\theta_3\), \(\theta_4\), and the coordinates of C) as a function of the known parameters.
Vector Loop Formulation#
We model the mechanism as a closed chain of position vectors. Starting from \(O_2\) and returning to \(O_2\), the sum of the vectors must be zero. \( \vec{L}_2 + \vec{L}_3 - \vec{L}_4 - \vec{L}_1 = 0 \) We rearrange the equation to isolate the vectors with the unknowns: \( \vec{L}_2 + \vec{L}_3 = \vec{L}_1 + \vec{L}_4 \) Now, we decompose this vector equation into its scalar components (x and y):
x-component (real): \( L_2\cos\theta_2 + L_3\cos\theta_3 = L_1 + L_4\cos\theta_4 \quad (\text{Equation 1}) \)
y-component (imaginary): \( L_2\sin\theta_2 + L_3\sin\theta_3 = L_4\sin\theta_4 \quad (\text{Equation 2}) \)
We have a system of two nonlinear equations with two unknowns, \(\theta_3\) and \(\theta_4\).
Solving for \(\theta_3\) and \(\theta_4\)#
One way to solve the system is by using Freudenstein’s Equation, which relates the input and output angles: \( K_1\cos\theta_3 + K_2\cos\theta_2 + K_3 = \cos(\theta_2 - \theta_3) \) Where the constants \(K_1, K_2, K_3\) depend only on the link lengths:
\(K_1 = L_1 / L_2\)
\(K_2 = L_1 / L_4\)
\(K_3 = (L_2^2 - L_3^2 + L_4^2 + L_1^2) / (2L_2L_4)\)
Solving the system for \(\theta_3\) and \(\theta_4\) yields an equation of the form \(A\cos\theta_3 + B\sin\theta_3 = C\), which has standard solutions. The final solutions are: \( \theta_4 = 2 \arctan\left(\frac{-B \pm \sqrt{B^2 - 4AC}}{2A}\right) \) \( \theta_3 = \arctan\left(\frac{L_4\sin\theta_4 - L_2\sin\theta_2}{L_1 + L_4\cos\theta_4 - L_2\cos\theta_2}\right) \) Where:
\(A = \cos\theta_2 - K_1 - K_2\cos\theta_2 + K_3\)
\(B = -2\sin\theta_2\)
\(C = K_1 - (K_2+1)\cos\theta_2 + K_3\)
The \(\pm\) sign in the square root gives us the two solutions corresponding to the open and crossed configurations.
Calculation of the Coordinates of Point C#
Once \(\theta_3\) and \(\theta_4\) are calculated:
Coordinates of A:
\(x_A = L_2\cos\theta_2\)
\(y_A = L_2\sin\theta_2\)
Coordinates of C: Point C is on link 3. Its position is defined by the vector \(\vec{R}_C = \vec{R}_A + \vec{R}_{AC}\). The vector \(\vec{R}_{AC}\) has a constant magnitude of 0.4 m and an angle that is the angle of link 3 (\(\theta_3\)) plus the fixed angle of \(30^\circ\) (\(\delta_3\)).
\(x_C = x_A + \overline{AC}\cos(\theta_3 + \delta_3)\)
\(y_C = y_A + \overline{AC}\sin(\theta_3 + \delta_3)\)
Numerical Calculation for the Example#
Next, the detailed numerical calculation is performed. It is crucial to clarify that the system has two mathematical solutions, which correspond to two different physical assemblies of the mechanism.
1. The Two Possible Configurations:
By solving the vector loop equations, two valid solutions are found:
Solution 1: Open Configuration
This is the configuration shown in the figure, where the polygon \(O_2ABO_4\) is convex and the links do not cross.
The angles are: \(\mathbf{\theta_3 \approx 34.18^\circ}\) and \(\mathbf{\theta_4 \approx 106.86^\circ}\).
This is the correct solution that matches GeoGebra.
Solution 2: Crossed Configuration
In this configuration, the coupler link (AB) would cross the frame (\(O_2O_4\)).
The angles are: \(\theta_3 \approx -59.04^\circ\) and \(\theta_4 \approx 228.21^\circ\).
This solution, although mathematically valid, does not correspond to the problem figure.
2. Calculation of Coordinates for the Open Configuration:
We use the angles from the correct configuration (the open one) for the calculations.
Initial Data:
Lengths: \(L_1=0.5, L_2=0.2, L_3=0.6, L_4=0.5, \overline{AC}=0.4\)
Angles: \(\theta_2 = 135^\circ\), \(\delta_3 = 30^\circ\)
Coordinates of A:
\(x_A = L_2\cos\theta_2 = 0.2 \cos(135^\circ) = -0.1414 \text{ m}\)
\(y_A = L_2\sin\theta_2 = 0.2 \sin(135^\circ) = 0.1414 \text{ m}\)
\(A = (-0.1414, 0.1414)\)
Coordinates of C: The absolute angle of the vector \(\vec{AC}\) is \(\theta_3 + \delta_3 = 34.18^\circ + 30^\circ = 64.18^\circ\).
\(x_C = x_A + \overline{AC}\cos(\theta_3 + \delta_3) = -0.1414 + 0.4\cos(64.18^\circ) = -0.1414 + 0.1742 = 0.0328 \text{ m}\)
\(y_C = y_A + \overline{AC}\sin(\theta_3 + \delta_3) = 0.1414 + 0.4\sin(64.18^\circ) = 0.1414 + 0.3601 = 0.5015 \text{ m}\)
\(C = (0.0328, 0.5015)\)
3. Final Verified Results:
\(\theta_3 = 34.18^\circ\)
\(\theta_4 = 106.86^\circ\)
Coordinates of C: (0.0328, 0.5015) m
Example 2.2 - Position Analysis of a Slider-Crank Mechanism#
The figure shows a slider-crank mechanism. For the instant when the crank forms an angle \(\theta_2 = 30^{\circ}\) with the horizontal, calculate the position of the slider and the angle that link 3 forms with the horizontal.
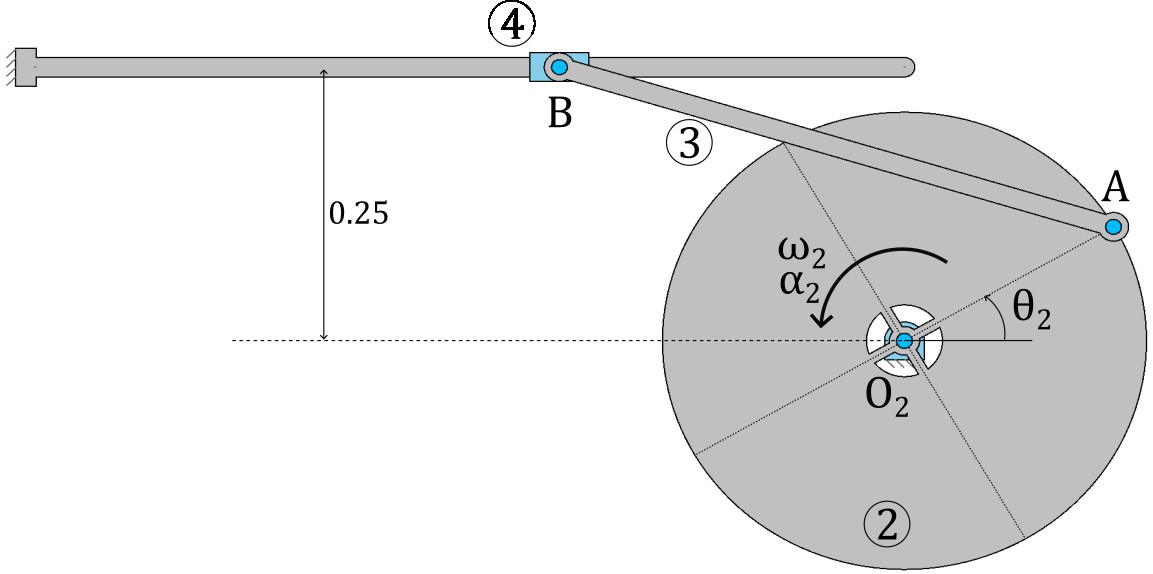
Data:
Link lengths, in meters: \(\overline{O_2 A} = 0.25;\,\overline{AB} = 0.6;\,y_B = 0.25;\)
Section 1: Position Analysis (Graphical Method)#
The objective is to construct the mechanism’s configuration to scale for the instant \(\theta_2 = 30^\circ\) and measure the position unknowns: the horizontal coordinate of the slider (\(x_B\)) and the angle of the coupler (\(\theta_3\)).
Construction Data:#
Link 2 (Crank): \(L_2 = \overline{O_2A} = 0.25 \text{ m}\)
Link 3 (Coupler): \(L_3 = \overline{AB} = 0.6 \text{ m}\)
Slider Axis: The slider moves on a horizontal line at a constant height \(y_B = 0.25 \text{ m}\).
Input Angle: \(\theta_2 = 30^\circ\).
Construction Procedure:#
Establish the origin: The fixed pivot \(O_2\) is placed at the coordinate origin (0,0).
Position the crank (Link 2): From \(O_2\), link 2 is drawn with its length \(L_2 = 0.25 \text{ m}\) and the input angle \(\theta_2 = 30^\circ\). The end of this vector is the position of joint A.
Draw the slider guide: The horizontal line that defines the path of slider B is drawn. This line is at a constant height \(y = 0.25 \text{ m}\).
Locate joint B (Loop closure):
Coupler Constraint: Point B must be at a distance \(L_3 = 0.6 \text{ m}\) from A. Geometrically, this is a circle with center A and radius 0.6.
Slider Constraint: Point B must lie on the line \(y = 0.25\).
Resolve configuration ambiguity: The intersection of the circle (center A, radius \(L_3\)) and the line (\(y=0.25\)) yields two possible solutions for point B. The one corresponding to the configuration shown in the problem figure must be chosen.
Measurement of results: With the mechanism fully drawn, the desired quantities are measured directly from the graphical software:
Coordinates of point B: \((x_B, y_B)\).
Angle of the coupler, \(\theta_3\): The angle of the segment AB with the horizontal.
Section 2: Position Analysis (Analytical Method)#
The objective is to find expressions for the unknowns (\(x_B\) and \(\theta_3\)) as a function of the known parameters.
Vector Loop Formulation#
We model the mechanism as an open vector chain. The position of point B can be expressed starting from the origin \(O_2\): \( \vec{R}_B = \vec{R}_A + \vec{R}_{AB} \) Where:
\(\vec{R}_A = L_2(\cos\theta_2 \hat{i} + \sin\theta_2 \hat{j})\)
\(\vec{R}_{AB} = L_3(\cos\theta_3 \hat{i} + \sin\theta_3 \hat{j})\)
\(\vec{R}_B = x_B \hat{i} + y_B \hat{j}\) (with \(y_B\) constant)
We decompose the vector equation into its scalar components (x and y):
x-component: \( x_B = L_2\cos\theta_2 + L_3\cos\theta_3 \quad (\text{Equation 1}) \)
y-component: \( y_B = L_2\sin\theta_2 + L_3\sin\theta_3 \quad (\text{Equation 2}) \)
We have a system of two equations with two unknowns: \(\theta_3\) and \(x_B\).
Solving for \(\theta_3\) and \(x_B\)#
Solve for \(\theta_3\): From Equation 2, we can solve for \(\sin\theta_3\): \( \sin\theta_3 = \frac{y_B - L_2\sin\theta_2}{L_3} \) This will give us two possible values for \(\theta_3\), since \(\theta_{3,2} = 180^\circ - \theta_{3,1}\). We must choose the solution that corresponds to the configuration in the drawing. Once \(\sin\theta_3\) is known, we can find \(\cos\theta_3 = \pm\sqrt{1 - \sin^2\theta_3}\), where the sign depends on the quadrant in which \(\theta_3\) lies.
Solve for \(x_B\): Once we have the correct value of \(\theta_3\) (and therefore, of \(\cos\theta_3\)), we substitute it into Equation 1 to find the position of the slider: \( x_B = L_2\cos\theta_2 + L_3\cos\theta_3 \)
Numerical Calculation for the Example#
The calculation is performed for the two possible configurations.
Initial Data:
Lengths: \(L_2=0.25 \text{ m}, L_3=0.6 \text{ m}\)
Vertical position of the slider: \(y_B = 0.25 \text{ m}\)
Input angle: \(\theta_2 = 30^\circ\)
Calculation of \(\theta_3\): Using Equation 2: \( \sin\theta_3 = \frac{0.25 - 0.25\sin(30^\circ)}{0.6} = \frac{0.25 - 0.25 \cdot 0.5}{0.6} = \frac{0.125}{0.6} \approx 0.2083 \) This gives two possible solutions for \(\theta_3\):
Solution 1: \(\theta_{3,1} = \arcsin(0.2083) \approx 12.02^\circ\). This corresponds to the configuration in the figure.
Solution 2: \(\theta_{3,2} = 180^\circ - 12.02^\circ = 167.98^\circ\). This corresponds to the other possible configuration of the mechanism.
Calculation of \(x_B\) (for Solution 2): The second solution for \(\theta_3\) is chosen. First, we calculate the cosine for this angle: \( \cos(167.98^\circ) \approx -0.9781 \) Now, we use Equation 1: \( x_B = 0.25\cos(30^\circ) + 0.6\cos(167.98^\circ) = 0.25 \cdot 0.866 + 0.6 \cdot (-0.9781) \) \( x_B = 0.2165 - 0.5868 = -0.3703 \text{ m} \)
Final Position Results (Solution 2):
Coupler angle: \(\mathbf{\theta_3 = 167.98^\circ}\)
Slider position: \(\mathbf{x_B = -0.3703 \text{ m}}\)
Example 2.3 - Position Analysis of a Quick-Return Mechanism#
The figure shows a 4-bar quick-return mechanism. At the instant when the crank forms an angle \(\theta_2 = 20^{\circ}\) with the horizontal, calculate the relative position of the slider with respect to \(O_4\), the angle that link 4 forms with the horizontal, and the coordinates of point B.

Data:
Link lengths, in meters: \(\overline{O_2 A} = 1.0;\, \overline{O_4 B} = 3.0;\, \overline{O_2 O_4} = 3.0;\)
Section 1: Position Analysis (Graphical Method)#
The objective is to construct the mechanism to scale to measure the unknowns: the angle of link 4 (\(\theta_4\)), the position of slider A along link 4 (distance \(\overline{O_4A}\)), and the coordinates of point B.
Construction Data:#
Link 1 (Frame): \(L_1 = \overline{O_2O_4} = 3.0 \text{ m}\)
Link 2 (Crank): \(L_2 = \overline{O_2A} = 1.0 \text{ m}\)
Link 4 (Slotted bar): The total length is \(L_4 = \overline{O_4B} = 3.0 \text{ m}\).
Input Angle: \(\theta_2 = 20^\circ\).
Construction Procedure:#
Establish the frame: Place the fixed pivot \(O_2\) at the origin (0,0) and the fixed pivot \(O_4\) at (3, 0).
Position the crank (Link 2): From \(O_2\), draw link 2 with its length \(L_2 = 1.0 \text{ m}\) and angle \(\theta_2 = 20^\circ\). The end is the position of pin A.
Determine the slotted bar (Link 4): Draw a straight line passing through \(O_4\) and A. This line defines the orientation of link 4.
Locate point B: Extend the line from \(O_4\) in the direction of A until it has the total length of link 4, \(L_4 = 3.0 \text{ m}\). The end of this segment is point B.
Measurement of results:
Measure the angle of the line \(O_4B\) with the horizontal to get \(\theta_4\).
Measure the distance of the segment \(\overline{O_4A}\) to get the relative position of the slider.
Read the coordinates of point B from the reference system.
Section 2: Position Analysis (Analytical Method)#
Vector equations are used to find expressions for the unknowns (\(\theta_4\), \(d = \overline{O_4A}\), and coordinates of B).
Vector Loop Formulation#
We consider the loop formed by points \(O_2, O_4, A\). The vector equation is: \( \vec{R}_{O_2A} = \vec{R}_{O_2O_4} + \vec{R}_{O_4A} \) Rearranging to solve for the vector defining link 4: \( \vec{R}_{O_4A} = \vec{R}_{O_2A} - \vec{R}_{O_2O_4} \) Where:
\(\vec{R}_{O_2A} = L_2(\cos\theta_2 \hat{i} + \sin\theta_2 \hat{j})\)
\(\vec{R}_{O_2O_4} = L_1 \hat{i}\)
\(\vec{R}_{O_4A}\) is a vector whose direction gives us \(\theta_4\) and whose magnitude is the distance \(d = \overline{O_4A}\).
Solving for \(\theta_4\) and \(d\)#
Decompose into components: \( (x_A - x_{O_4}) \hat{i} + (y_A - y_{O_4}) \hat{j} = (L_2\cos\theta_2 - L_1) \hat{i} + (L_2\sin\theta_2) \hat{j} \)
Calculate \(\theta_4\): The angle of link 4 is the angle of the vector \(\vec{R}_{O_4A}\). \( \theta_4 = \arctan\left(\frac{L_2\sin\theta_2}{L_2\cos\theta_2 - L_1}\right) \)
Calculate \(d\) (slider position): The distance is the magnitude of the vector \(\vec{R}_{O_4A}\). \( d = |\vec{R}_{O_4A}| = \sqrt{(L_2\cos\theta_2 - L_1)^2 + (L_2\sin\theta_2)^2} \)
Calculation of the Coordinates of Point B#
Point B is at the end of link 4. Its position vector is: \( \vec{R}_B = \vec{R}_{O_4} + L_4 (\cos\theta_4 \hat{i} + \sin\theta_4 \hat{j}) \)
\(x_B = x_{O_4} + L_4\cos\theta_4\)
\(y_B = y_{O_4} + L_4\sin\theta_4\)
Numerical Calculation for the Example#
Initial Data:
Lengths: \(L_1=3.0 \text{ m}, L_2=1.0 \text{ m}, L_4=3.0 \text{ m}\)
Input angle: \(\theta_2 = 20^\circ\)
Calculation of \(\theta_4\) and \(d\): First, we calculate the components of the vector \(\vec{R}_{O_4A}\):
x-component: \(L_2\cos\theta_2 - L_1 = 1.0\cos(20^\circ) - 3.0 = 0.9397 - 3.0 = -2.0603 \text{ m}\)
y-component: \(L_2\sin\theta_2 = 1.0\sin(20^\circ) = 0.3420 \text{ m}\)
Now, we calculate the angle and magnitude: \( \theta_4 = \arctan\left(\frac{0.3420}{-2.0603}\right) = 170.56^\circ \) \( d = \sqrt{(-2.0603)^2 + (0.3420)^2} = \sqrt{4.2448 + 0.1170} = 2.0885 \text{ m} \)
Calculation of Coordinates of B: We use \(\theta_4 = 170.56^\circ\) and \(L_4 = 3.0 \text{ m}\).
\(x_B = 3.0 + 3.0\cos(170.56^\circ) = 3.0 + 3.0(-0.9865) = 3.0 - 2.9595 = 0.0405 \text{ m}\)
\(y_B = 0 + 3.0\sin(170.56^\circ) = 3.0(0.1640) = 0.4920 \text{ m}\)
Final Position Results:
Slider position A: \(\mathbf{d = \overline{O_4A} = 2.089 \text{ m}}\)
Angle of link 4: \(\mathbf{\theta_4 = 170.56^\circ}\)
Coordinates of B: (0.0405, 0.4920) m
Example 2.4 - Position Analysis of an Inverted Slider-Crank Mechanism#
The figure shows an inverted slider-crank mechanism. At the instant when the crank forms an angle \(\theta_2 = 60^{\circ}\) with the horizontal, calculate the position of the slider with respect to point A, the angles that links 3 and 4 form with the horizontal, and the coordinates of point C.
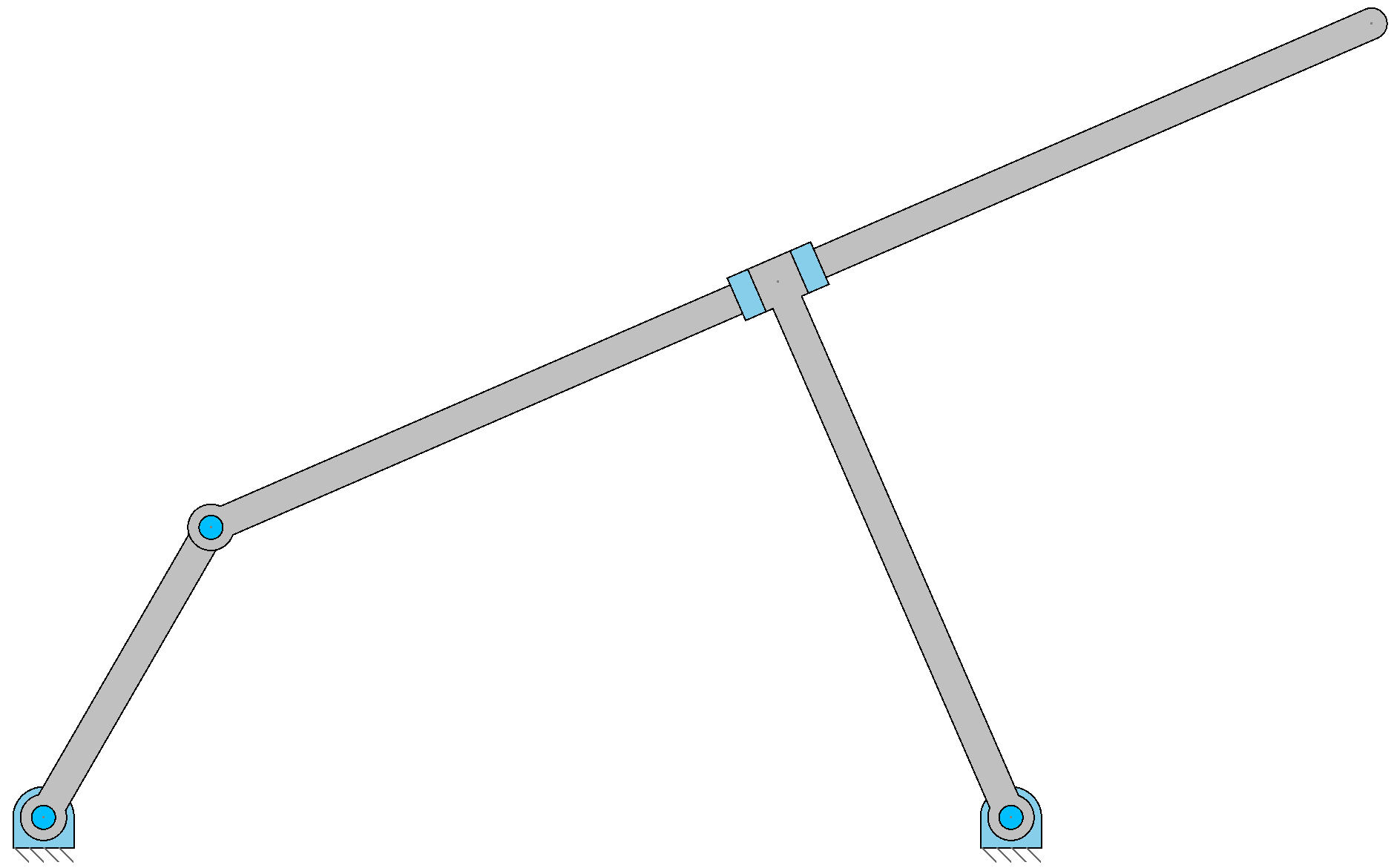
Data:
Link lengths, in meters: \(\overline{O_2 A} = 0.45;\, \overline{AC} = 1.7;\, \overline{O_4B} = 0.7855;\) the angle \(\gamma\) that links 3 and 4 form is \(90^\circ\).
Section 1: Position Analysis (Graphical Method)#
The objective is to construct the mechanism to scale to measure the unknowns: the distance of the slider to point A (\(\overline{AB}\)), the angles \(\theta_3\) and \(\theta_4\), and the coordinates of point C.
Construction Data:#
Link 1 (Frame): Distance \(\overline{O_2O_4} = L_1 = 1.30 \text{ m}\)
Link 2 (Crank): \(L_2 = \overline{O_2A} = 0.45 \text{ m}\).
Link 3 (Coupler): Point C is at a distance \(\overline{AC} = 1.7 \text{ m}\) from A.
Link 4 (Rocker): The perpendicular distance from \(O_4\) to the slot is \(h = \overline{O_4B} = 0.7855 \text{ m}\).
Input Angle: \(\theta_2 = 60^\circ\).
Geometric Constraint: The angle between the line \(AC\) (link 3) and the line \(O_4B\) (link 4) is \(90^\circ\).
Construction Procedure:#
Establish the frame: Locate pivot \(O_2\) at the origin (0,0) and pivot \(O_4\) at \((L_1, 0)\).
Position the crank: Draw link 2 from \(O_2\) with length \(L_2=0.45\) and angle \(\theta_2=60^\circ\) to find point A.
Draw the slot (Link 3):
Draw a circle with center \(O_4\) and radius \(h = 0.7855\).
Draw a straight line starting from A and tangent to this circle. This defines the direction of link 3 and its angle \(\theta_3\). There are two possible tangents, choose the one corresponding to the figure.
Locate point B: Point B is the point of tangency between the line and the circle.
Locate point C: On the line passing through A and B, measure a distance \(\overline{AC} = 1.7\) from A to find C.
Determine link 4: Draw the line connecting \(O_4\) and B. Its angle is \(\theta_4\).
Measurement of results: Measure from the drawing the distance \(\overline{AB}\), the angles \(\theta_3\) and \(\theta_4\), and the coordinates of C.
Section 2: Position Analysis (Analytical Method)#
Vector Loop Formulation#
We consider the triangle formed by points \(O_2, O_4, A\). The distance between \(O_4\) and A, \(d_{O_4A}\), can be calculated with the law of cosines: \( d_{O_4A}^2 = L_1^2 + L_2^2 - 2L_1L_2\cos\theta_2 \) In the right triangle \(O_4BA\), we have: \( d_{O_4A}^2 = (\overline{O_4B})^2 + (\overline{AB})^2 = h^2 + (\overline{AB})^2 \) Equating both expressions, we can solve for the distance \(\overline{AB}\) (position of the slider with respect to A): \( \overline{AB} = \sqrt{L_1^2 + L_2^2 - 2L_1L_2\cos\theta_2 - h^2} \)
Solving for \(\theta_3\) and \(\theta_4\)#
Calculate angle \(\alpha = \angle AO_4O_2\): Using the law of sines in triangle \(O_2O_4A\): \( \frac{\sin\alpha}{L_2} = \frac{\sin\theta_2}{d_{O_4A}} \implies \alpha = \arcsin\left(\frac{L_2\sin\theta_2}{d_{O_4A}}\right) \)
Calculate angle \(\beta = \angle AO_4B\): Using the right triangle \(O_4BA\): \( \cos\beta = \frac{\overline{O_4B}}{d_{O_4A}} = \frac{h}{d_{O_4A}} \implies \beta = \arccos\left(\frac{h}{d_{O_4A}}\right) \)
Calculate \(\theta_3\) and \(\theta_4\): Observing the geometry of the mechanism: \( \theta_3 = 180^\circ - (\alpha + \beta) \) Since \(\vec{O_4B}\) is perpendicular to the line AC (link 3): \( \theta_4 = \theta_3 - 90^\circ \)
Calculation of the Coordinates of Point C#
\( \vec{R}_C = \vec{R}_A + \vec{R}_{AC} \)
\(x_C = L_2\cos\theta_2 + \overline{AC}\cos\theta_3\)
\(y_C = L_2\sin\theta_2 + \overline{AC}\sin\theta_3\)
Numerical Calculation#
Initial Data:
\(L_1 = 1.3 \text{ m}\)
\(L_2 = 0.45 \text{ m}\)
\(\overline{AC} = 1.7 \text{ m}\)
\(h = \overline{O_4B} = 0.7855 \text{ m}\)
\(\theta_2 = 60^\circ\)
1. Calculate distance \(d_{O_4A}\) and slider position \(\overline{AB}\): \( d_{O_4A}^2 = 1.3^2 + 0.45^2 - 2(1.3)(0.45)\cos(60^\circ) = 1.69 + 0.2025 - 0.585 = 1.3075 \) \( d_{O_4A} = \sqrt{1.3075} \approx 1.143 \text{ m} \) \( \overline{AB} = \sqrt{d_{O_4A}^2 - h^2} = \sqrt{1.3075 - 0.7855^2} = \sqrt{0.6904} \approx 0.831 \text{ m} \)
2. Calculate angle of vector \(\vec{R}_{O_4A}\) (\(\phi\)) and angle \(\beta\): The angle \(\phi\) is that of the vector from \(O_4\) to A. \( \phi = \arctan\left(\frac{y_A - y_{O_4}}{x_A - x_{O_4}}\right) = \arctan\left(\frac{L_2\sin\theta_2}{L_2\cos\theta_2 - L_1}\right) = \arctan\left(\frac{0.45\sin(60^\circ)}{0.45\cos(60^\circ) - 1.3}\right) \) \( \phi = \arctan\left(\frac{0.3897}{-1.075}\right) \approx 160.05^\circ \) The angle \(\beta\) is from the right triangle \(O_4BA\). \( \beta = \arccos\left(\frac{h}{d_{O_4A}}\right) = \arccos\left(\frac{0.7855}{1.143}\right) \approx 46.59^\circ \)
3. Calculate \(\theta_3\) and \(\theta_4\): From the geometry, it is observed that the angle of link 4, \(\theta_4\), is the sum of angles \(\phi\) and \(\beta\) (considering the quadrant). The configuration in the figure corresponds to: \( \theta_4 = \phi - \beta = 160.05^\circ - 46.59^\circ = 113.46^\circ \) And the angle of link 3 (the slot) is perpendicular to link 4: \( \theta_3 = \theta_4 - 90^\circ = 113.46^\circ - 90^\circ = 23.46^\circ \)
4. Calculate Coordinates of Point C: \( x_C = L_2\cos\theta_2 + \overline{AC}\cos\theta_3 = 0.45\cos(60^\circ) + 1.7\cos(23.46^\circ) = 0.225 + 1.559 = 1.784 \text{ m} \) \( y_C = L_2\sin\theta_2 + \overline{AC}\sin\theta_3 = 0.45\sin(60^\circ) + 1.7\sin(23.46^\circ) = 0.3897 + 0.677 = 1.067 \text{ m} \)
Final Position Results:
Slider position: \(\mathbf{\overline{AB} = 0.831 \text{ m}}\)
Angle of link 3: \(\mathbf{\theta_3 = 23.46^\circ}\)
Angle of link 4: \(\mathbf{\theta_4 = 113.46^\circ}\)
Coordinates of C: (1.784, 1.067) m
Example 2.5 - Position Analysis of a 6-Bar Linkage#
The figure shows a 6-bar linkage. At the instant when the crank forms an angle \(\theta_2 = 225^{\circ}\) with the horizontal, calculate the position of the slider, the angle that the segment \(O_4B\) forms with the horizontal, and the coordinates of point C.
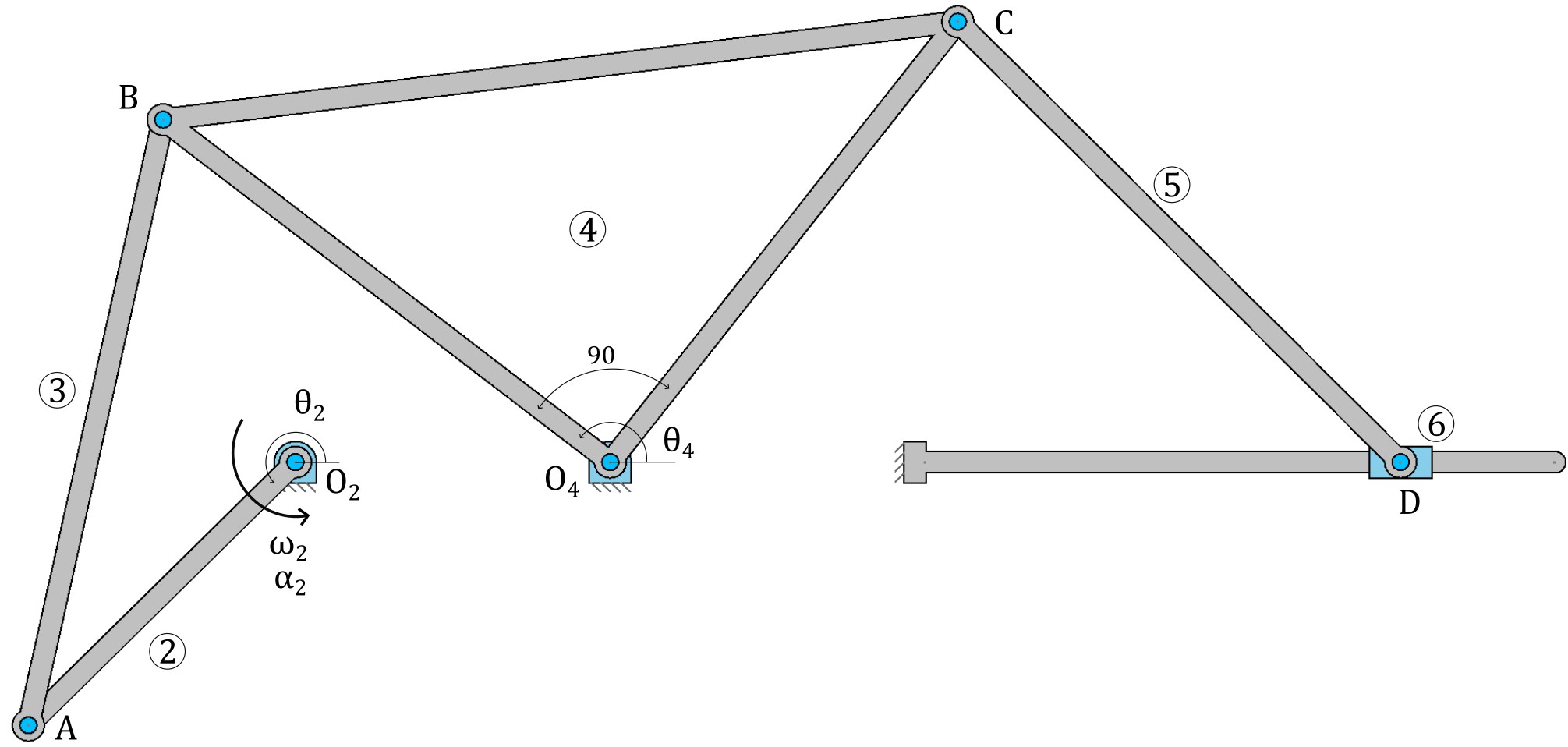
Data:
Link lengths, in meters: \(\overline{O_2 A} = 0.30;\, \overline{AB} = 0.5;\, \overline{O_4B} = \overline{O_4C} = 0.45;\, \overline{C D} = 0.50;\) the angle \(\gamma\) between \(\overline{O_4B}\) and \(\overline{O_4C}\) is \(90^\circ\). \(\overline{O_2 O_4} = 0.25;\) The slider moves horizontally on the x-axis.
Section 1: Position Analysis (Graphical Method)#
The objective is to construct the mechanism to scale to measure the unknowns: the angle \(\theta_4\), the coordinates of point C, and the position of slider D.
Construction Procedure:#
Locate the fixed pivots: Place \(O_2\) at the origin (0,0) and \(O_4\) at (0.25, 0).
Position the crank (Link 2): From \(O_2\), draw link 2 with a length of 0.30 m and an angle \(\theta_2 = 225^\circ\) to find point A.
Close the first loop (4-bar):
Draw a circle with center A and radius \(\overline{AB} = 0.5\) m.
Draw a circle with center \(O_4\) and radius \(\overline{O_4B} = 0.45\) m.
The intersection of both circles gives the position of point B. Choose the solution that corresponds to the figure.
Locate point C:
Draw the line connecting \(O_4\) and B.
Rotate this line \(90^\circ\) clockwise around \(O_4\).
On this new line, measure a distance \(\overline{O_4C} = 0.45\) m from \(O_4\) to find point C.
Locate slider D:
Draw a circle with center C and radius \(\overline{CD} = 0.50\) m.
The intersection of this circle with the horizontal axis (x-axis) gives the position of slider D. Choose the solution that corresponds to the figure.
Measurement of results: Measure in the graphical software the angle of the bar \(O_4B\) (\(\theta_4\)), the coordinates of C, and the x-coordinate of D.
Section 2: Position Analysis (Analytical Method)#
The problem is solved in two parts: first the four-bar loop \(O_2ABO_4\) and then the dyad \(O_4CD\).
Vector Loop Formulation (Loop 1: \(O_2ABO_4\))#
The loop equation is \(\vec{L}_2 + \vec{L}_3 = \vec{L}_1 + \vec{L}_4\). Decomposing into x and y components:
\(L_2\cos\theta_2 + L_3\cos\theta_3 = L_1 + L_4\cos\theta_4\)
\(L_2\sin\theta_2 + L_3\sin\theta_3 = L_4\sin\theta_4\)
Rearranging and squaring to eliminate \(\theta_3\), we arrive at an equation of the form \(A\cos\theta_4 + B\sin\theta_4 = C\), which allows solving for \(\theta_4\).
Numerical Calculation#
Initial Data:
\(L_1 = \overline{O_2O_4} = 0.25 \text{ m}\)
\(L_2 = \overline{O_2A} = 0.30 \text{ m}\)
\(L_3 = \overline{AB} = 0.5 \text{ m}\)
\(L_4 = \overline{O_4B} = 0.45 \text{ m}\)
\(\overline{O_4C} = 0.45 \text{ m}\)
\(\overline{CD} = 0.50 \text{ m}\)
\(\theta_2 = 225^\circ\)
\(\gamma = 90^\circ\) (angle \(\angle BO_4C\), clockwise)
1. Solve the 4-bar loop (\(O_2ABO_4\)): Freudenstein’s equation is solved for \(\theta_4\). The constants are:
\(A = 2L_1L_4 - 2L_2L_4\cos\theta_2 = 2(0.25)(0.45) - 2(0.3)(0.45)\cos(225^\circ) = 0.4159\)
\(B = -2L_2L_4\sin\theta_2 = -2(0.3)(0.45)\sin(225^\circ) = 0.1909\)
\(C = L_3^2 - L_1^2 - L_2^2 - L_4^2 + 2L_1L_2\cos\theta_2 = 0.5^2 - 0.25^2 - 0.3^2 - 0.45^2 + 2(0.25)(0.3)\cos(225^\circ) = -0.2111\)
Solving \(0.4159\cos\theta_4 + 0.1909\sin\theta_4 = -0.2111\) yields two solutions. The one corresponding to the figure is:
\(\mathbf{\theta_4 = 142.13^\circ}\)
2. Calculate the position of point C: The link \(\overline{O_4C}\) forms an angle \(\theta_C\) with the horizontal. Since the angle \(\gamma = \angle BO_4C\) is \(90^\circ\) clockwise (subtracting from the angle of bar 4): \( \theta_C = \theta_4 - \gamma = 142.13^\circ - 90^\circ = 52.13^\circ \) The coordinates of C are (relative to \(O_4\) which is at (0.25, 0)): \( x_C = x_{O_4} + \overline{O_4C}\cos\theta_C = 0.25 + 0.45\cos(52.13^\circ) = 0.25 + 0.276 = 0.526 \text{ m} \) \( y_C = y_{O_4} + \overline{O_4C}\sin\theta_C = 0 + 0.45\sin(52.13^\circ) = 0.355 \text{ m} \)
Coordinates of C: (0.526, 0.355) m
3. Calculate the position of slider D: Point D is on the x-axis (\(y_D=0\)). The distance \(\overline{CD}\) is \(0.50 \text{ m}\). Using the Pythagorean theorem in the triangle formed by C, D, and the projection of C on the x-axis: \( (\overline{CD})^2 = (x_C - x_D)^2 + (y_C - y_D)^2 \) \( 0.5^2 = (0.526 - x_D)^2 + (0.355 - 0)^2 \) \( 0.25 = (0.526 - x_D)^2 + 0.126 \) \( (0.526 - x_D)^2 = 0.124 \implies 0.526 - x_D = \pm\sqrt{0.124} = \pm 0.352 \) The two possible solutions for \(x_D\) are \(x_D = 0.526 \mp 0.352\). The one corresponding to the figure (further to the right) is:
Position of slider D: \(x_D = 0.878 \text{ m}\)
Final Position Results:
Angle of link 4: \(\mathbf{\theta_4 = 142.13^\circ}\)
Coordinates of C: (0.526, 0.355) m
Position of slider D: \(\mathbf{x_D = 0.878}\)
Example 2.6 - Velocity Analysis of a Four-Bar Linkage#
For the mechanism in Example 2.1, at the instant when \(\theta_2 = 135^{\circ}\), the angular velocity of the input link is \(\vec{\omega}_2 = 2\hat{k}\) rad/s. Calculate the velocity of point C and the angular velocity of link 4.
Data from position analysis: \(\theta_3 = 34.18^{\circ};\, \theta_4 = 106.86^{\circ}\) \(\vec{r}_{O2A} = -0.141\hat{i} + 0.141\hat{j}\) \(\vec{r}_{AB} = 0.496\hat{i} + 0.337\hat{j}\) \(\vec{r}_{O4B} = -0.145\hat{i} + 0.478\hat{j}\) \(\vec{r}_{AC} = 0.174\hat{i} + 0.360\hat{j}\)
Resolution#
We start by finding the velocity of point A: \(\vec{v}_A = \vec{\omega}_2 \times \vec{r}_{O2A} = 2\hat{k} \times (-0.141\hat{i} + 0.141\hat{j}) = -0.282\hat{i} - 0.282\hat{j}\) m/s.
Now we write the relative velocity equation for point B: \(\vec{v}_B = \vec{v}_A + \vec{v}_{B/A} = \vec{v}_A + \vec{\omega}_3 \times \vec{r}_{AB}\) \(\vec{v}_B = -0.282\hat{i} - 0.282\hat{j} + \omega_3\hat{k} \times (0.496\hat{i} + 0.337\hat{j})\) \(\vec{v}_B = -0.282\hat{i} - 0.282\hat{j} - 0.337\omega_3\hat{i} + 0.496\omega_3\hat{j}\) \(\vec{v}_B = (-0.282 - 0.337\omega_3)\hat{i} + (-0.282 + 0.496\omega_3)\hat{j}\)
We also express \(\vec{v}_B\) from link 4: \(\vec{v}_B = \vec{\omega}_4 \times \vec{r}_{O4B} = \omega_4\hat{k} \times (-0.145\hat{i} + 0.478\hat{j})\) \(\vec{v}_B = -0.478\omega_4\hat{i} - 0.145\omega_4\hat{j}\)
Equating the two expressions for \(\vec{v}_B\): \(-0.282 - 0.337\omega_3 = -0.478\omega_4\) \(-0.282 + 0.496\omega_3 = -0.145\omega_4\)
Solving the system of two equations for \(\omega_3\) and \(\omega_4\): \(0.478\omega_4 - 0.337\omega_3 = 0.282\) \(0.145\omega_4 + 0.496\omega_3 = 0.282\)
This yields: \(\omega_3 = 0.328\) rad/s \(\omega_4 = 0.821\) rad/s
So, \(\vec{\omega}_3 = 0.328\hat{k}\) rad/s and \(\vec{\omega}_4 = 0.821\hat{k}\) rad/s.
Finally, we calculate the velocity of point C: \(\vec{v}_C = \vec{v}_A + \vec{v}_{C/A} = \vec{v}_A + \vec{\omega}_3 \times \vec{r}_{AC}\) \(\vec{v}_C = -0.282\hat{i} - 0.282\hat{j} + 0.328\hat{k} \times (0.174\hat{i} + 0.360\hat{j})\) \(\vec{v}_C = -0.282\hat{i} - 0.282\hat{j} - 0.118\hat{i} + 0.057\hat{j}\) \(\vec{v}_C = -0.400\hat{i} - 0.225\hat{j}\) m/s.
Velocity Kinematics (Cinema)#
The following GeoGebra model shows the velocity cinema of the mechanism.
Note that to calculate the velocity of point C, one can use the concept of homology between the velocity cinema and the mechanism (a rotation of \(90^\circ\) and scaling). This way, it’s possible to find point \(c\) in the velocity cinema, which defines the end of a vector originating from \(O_v\) that determines the velocity of C, \(\vec{v}_C\). This point is found at a distance \(\overline{ac}=\frac{\overline{ab}}{\overline{AB}}\overline{AC}\) on the segment \(ab\), and is then rotated 30 degrees counter-clockwise, as was done to obtain point C in the mechanism’s construction.
Example 2.7 - Velocity Analysis of a Slider-Crank Mechanism#
The figure shows a slider-crank mechanism. At the instant when the crank forms an angle \(\theta_2 = 30^{\circ}\) with the horizontal, its angular velocity is \(\vec{\omega}_2 = 1\hat{k}\) rad/s, and its acceleration is \(\vec{\alpha}_2 = 1\hat{k}\) rad/s². Calculate the velocity of the slider and the angular velocity of link 3.

Data:
Link lengths, in meters: \(\overline{O_2 A} = 0.25;\, \overline{AB} = 0.6;\, y_B = 0.25\). Angle of link 3 with the horizontal, from the position analysis: \(\theta_3 = 167.98^{\circ}\).
Resolution (Calculations in Matlab)#
For this example, we will perform the calculations using Matlab. We start by creating variables for the given data:
clear, clc
O2A = 0.25; AB = 0.6;
th2 = 30; th3 = 167.98;
w2 = [0 0 1]; af2 = [0 0 1];
The mechanism has one degree of freedom, corresponding to \(\vec{\omega}_2\). We use this known data to calculate the velocity of point A:
\(\vec{v}_A = \vec{\omega}_2 \times \vec{r}_{O2A}\)
From the geometric data, we calculate \(\vec{r}_{O2A}\):
rO2A = O2A * [cosd(th2) sind(th2) 0];
Therefore,
\(\vec{v}_A = 1\hat{k} \times (0.2165\hat{i} + 0.125\hat{j}) = -0.125\hat{i} + 0.2165\hat{j}\)
vA = cross(w2, rO2A);
Next, we focus on point B. Analyzing it as part of link 3, we can establish the relative velocity equation between A and B:
\(\vec{v}_{B3} = \vec{v}_A + \vec{v}_{B/A}\)
with \(\vec{v}_A\) known and \(\vec{v}_{B/A} = \vec{\omega}_3 \times \vec{r}_{AB}\), where we know the direction but not the magnitude of \(\vec{\omega}_3\).
syms w3k real
w3 = [0 0 w3k];
rAB = AB * [cosd(th3) sind(th3) 0];
vB_A = cross(w3, rAB);
vB3 = vA + vB_A;
Now we analyze point B as part of link 4 (the slider). Since it’s a slider, we know its direction must be along the sliding axis, which is horizontal in this case:
\(\vec{v}_{B4} = v_B\hat{i}\)
syms vBi real
vB4 = [vBi 0 0];
Since there is a revolute joint at B, we can equate the two expressions:
sol_v1 = solve(vB3 == vB4, w3k, vBi);
w3k = double(sol_v1.w3k);
vBi = double(sol_v1.vBi);
fprintf('w3k=%0.3f vBi=%0.3f\n', w3k, vBi)
w3k=0.369 vBi=-0.171
Velocity Cinema#
The velocity cinema for this example is not provided, but it can be created using the same principles demonstrated in previous examples.
Example 2.8 - Velocity Analysis of a Quick-Return Mechanism#
The figure shows a 4-bar quick-return mechanism, in which the slider represents the expansion movement of a cylinder (e.g., a truck’s hydraulic cylinder) at a constant velocity of \(0.1\) m/s. At the instant when the crank forms an angle \(\theta_2 = 20^{\circ}\) with the horizontal, calculate the velocity of point B and the angular velocities of links 2 and 4.

Data:
Link lengths, in meters: \(\overline{O_2 A} = 1.0;\, \overline{O_4 B} = 3.0;\, \overline{O_2 O_4} = 3.0\). Angle of link 4 with the horizontal, from Example 2.3 (position analysis): \(\theta_4 = 170.56^{\circ}\). Position of slider A relative to \(O_4\): \(d = \overline{O_4 A} = 2.089\) m.
Resolution#
The mechanism has one degree of freedom, which corresponds to the relative velocity of the slider with respect to link 4, \(\vec{v}_{A3/A4} = \vec{v}_{A2/A4}\). We use this known data to calculate the angular velocities of links 2 and 4 by applying the relative velocity equation, knowing that at the analyzed instant, points \(A_2\), \(A_3\), and \(A_4\) coincide. It’s worth remembering that \(A_2\) and \(A_3\), being connected by a revolute joint, have the same absolute velocity, which must be perpendicular to link 2. Meanwhile, 3 and 4 are joined by a prismatic joint, and between \(A_3\) and \(A_4\) there is a relative velocity in the direction of link 4, which is precisely the data provided. With this, we have:
\(\vec{v}_{A_2} = \vec{v}_{A_4} + \vec{v}_{A_2/A_4}\)
where each term can be expressed as:
\(\vec{v}_{A_2} = \vec{\omega}_2 \times \vec{r}_{O2A}\)
clear, clc
syms w2k real
rO2A = [cosd(20) sind(20) 0];
w2 = [0 0 w2k];
vA2 = cross(w2, rO2A);
\(\vec{v}_{A_4} = \vec{\omega}_4 \times \vec{r}_{O4A}\)
syms w4k real
rO4A = 2.089 * [cosd(170.56) sind(170.56) 0];
w4 = [0 0 w4k];
vA4 = cross(w4, rO4A);
\(\vec{v}_{A_2/A_4} = 0.1(\cos 170.56^{\circ} \hat{i} + \sin 170.56^{\circ} \hat{j})\)
vA2_A4 = 0.1 * [cosd(170.56) sind(170.56) 0];
Now we can solve the relative velocity equation:
eq1 = vA2 == vA4 + vA2_A4;
sol_v1 = solve(eq1, w2k, w4k);
w2k = double(sol_v1.w2k);
w4k = double(sol_v1.w4k);
fprintf('w2k=%0.3f w4k=%0.3f\n', w2k, w4k)
w2k=0.203 w4k=-0.085
Finally, we calculate the velocity of point B now that we know \(\vec{\omega}_4\):
rO4B = 3 * [cosd(170.56) sind(170.56) 0];
vB = subs(cross(w4, rO4B));
fprintf('|vB|=%0.3f\n', norm([vB(1) vB(2)]))
|vB|=0.254
Velocity Cinema#
The velocity cinema for this example is not provided, but it can be created using the same principles demonstrated in previous examples.
Example 2.11 - Acceleration Analysis of a Four-Bar Linkage#
The figure shows a 4-bar mechanism, whose position analysis was performed in Example 2.1 and velocities were calculated in Example 2.6. At the instant when the crank forms an angle \(\theta_2 = 135^{\circ}\) with the horizontal, its angular velocity is \(\vec{\omega}_2 = 2\hat{k}\) rad/s, and its acceleration is \(\vec{\alpha}_2 = -1.5\hat{k}\) rad/s². Calculate the acceleration of point C and the angular acceleration of link 4.

Data:
Link lengths, in meters: \(\overline{O_2 A} = 0.2;\, \overline{AB} = 0.6;\, \overline{O_4 B} = 0.5;\, \overline{O_2 O_4} = 0.5;\, \overline{AC} = 0.4\). Angles of links 3 and 4 with the horizontal (from position analysis): \(\theta_3 = 34.18^{\circ};\, \theta_4 = 106.86^{\circ}\). And their velocities (from velocity analysis): \(\vec{\omega}_3 = 0.328\hat{k}\) rad/s; \(\vec{\omega}_4 = 0.821\hat{k}\) rad/s.
Resolution#
The procedure for calculating the mechanism’s accelerations is similar to that for velocities. We start with point A as we have information about it. We calculate \(\vec{a}_A\) from its normal and tangential components:
\(\vec{a}_A = \vec{a}_A^n + \vec{a}_A^t = \vec{\omega}_2 \times (\vec{\omega}_2 \times \vec{r}_{O2A}) + \vec{\alpha}_2 \times \vec{r}_{O2A}\) \(\vec{a}_A = 2\hat{k} \times (2\hat{k} \times (-0.141\hat{i} + 0.141\hat{j})) - 1.5\hat{k} \times (-0.141\hat{i} + 0.141\hat{j}) = 0.777\hat{i} - 0.353\hat{j}\)
Now, analyzing point B as part of link 3, we have:
\(\vec{a}_B = \vec{a}_A + \vec{a}_{B/A}\)
which, by decomposing, gives:
\(\vec{a}_B^n + \vec{a}_B^t = \vec{a}_A + \vec{a}_{B/A}^n + \vec{a}_{B/A}^t\)
where the acceleration of A is known, and we can express the components of the relative acceleration from the available information:
For \(\vec{a}_{B/A}^n\), everything is known. Therefore: \(\vec{a}_{B/A}^n = \vec{\omega}_3 \times (\vec{\omega}_3 \times \vec{r}_{AB}) = -0.053\hat{i} - 0.036\hat{j}\)
For \(\vec{a}_{B/A}^t\), we can operate and express it in terms of the unknown \(\vec{\alpha}_3\), of which we only know its direction: \(\vec{a}_{B/A}^t = \vec{\alpha}_3 \times \vec{r}_{AB} = \alpha_3\hat{k} \times (0.496\hat{i} + 0.337\hat{j}) = -0.337\alpha_3\hat{i} + 0.496\alpha_3\hat{j}\)
On the other hand, if we consider point B as part of link 4, we have:
For \(\vec{a}_B^n\), of which we know everything: \(\vec{a}_B^n = \vec{\omega}_4 \times (\vec{\omega}_4 \times \vec{r}_{O4B}) = 0.098\hat{i} - 0.324\hat{j}\)
For \(\vec{a}_B^t\), of which we don’t know \(\vec{\alpha}_4\): \(\vec{a}_B^t = \vec{\alpha}_4 \times \vec{r}_{O4B} = \alpha_4\hat{k} \times (-0.145\hat{i} + 0.478\hat{j}) = -0.478\alpha_4\hat{i} - 0.145\alpha_4\hat{j}\)
Finally, if we equate both expressions, we have:
\(0.098\hat{i} - 0.324\hat{j} - 0.478\alpha_4\hat{i} - 0.145\alpha_4\hat{j} = 0.777\hat{i} - 0.353\hat{j} - 0.053\hat{i} - 0.036\hat{j} - 0.337\alpha_3\hat{i} + 0.496\alpha_3\hat{j}\)
From which it is possible to obtain a system of two equations with two unknowns, \(\alpha_3\) and \(\alpha_4\), once we decompose into \(\hat{i}\) and \(\hat{j}\):
\(0.098 - 0.478\alpha_4 = 0.777 - 0.053 - 0.337\alpha_3\) \(-0.324 - 0.145\alpha_4 = -0.353 - 0.036 + 0.496\alpha_3\)
whose solution gives us:
\(\alpha_3 = 0.427\) \(\alpha_4 = -1.007\)
which, knowing the direction, we can express in vector form:
\(\vec{\alpha}_3 = 0.427\hat{k}\) rad/s²; \(\vec{\alpha}_4 = -1.007\hat{k}\) rad/s²
Finally, to calculate the acceleration of point C, we apply relative accelerations between C and A:
\(\vec{a}_C = \vec{a}_A + \vec{a}_{C/A}^n + \vec{a}_{C/A}^t = 0.777\hat{i} - 0.353\hat{j} + \vec{\omega}_3 \times (\vec{\omega}_3 \times \vec{r}_{AC}) + \vec{\alpha}_3 \times \vec{r}_{AC}\) \(\vec{a}_C = 0.777\hat{i} - 0.353\hat{j} + 0.328\hat{k} \times (0.328\hat{k} \times (0.174\hat{i} + 0.360\hat{j})) + 0.427\hat{k} \times (0.174\hat{i} + 0.360\hat{j}) = 0.605\hat{i} - 0.318\hat{j}\) m/s²
Acceleration Cinema#
The following GeoGebra model shows the acceleration cinema of the mechanism.
Note that to calculate the acceleration of point C, one can use the concept of homology between the acceleration cinema and the mechanism (a rotation of \(180^\circ\) and scaling). This way, it’s possible to find point \(c'\) in the acceleration cinema, which defines the end of a vector originating from \(O_a\) that determines the acceleration of C, \(\vec{a}_C\). This point is found at a distance \(\overline{a'c'}=\frac{\overline{a'b'}}{\overline{AB}}\overline{AC}\) on the segment \(a'b'\), and is then rotated 30 degrees counter-clockwise, as was done to obtain point C in the mechanism’s construction.
Example 2.12 - Acceleration Analysis of a Slider-Crank Mechanism#
The figure shows a slider-crank mechanism. At the instant when the crank forms an angle \(\theta_2 = 30^{\circ}\) with the horizontal, its angular velocity is \(\vec{\omega}_2 = 1\hat{k}\) rad/s, and its acceleration is \(\vec{\alpha}_2 = 1\hat{k}\) rad/s². Calculate the acceleration of the slider and the angular acceleration of link 3.

Data:
Link lengths, in meters: \(\overline{O_2 A} = 0.25;\, \overline{AB} = 0.6;\, y_B = 0.25\). Angle of link 3 with the horizontal (from position analysis): \(\theta_3 = 167.98^{\circ}\), and its angular velocity \(\vec{\omega}_3 = 0.369\) rad/s.
Resolution (Calculations in Matlab)#
The procedure for calculating the mechanism’s accelerations is similar to that for velocities. We start with point A as we have information about it. We calculate \(\vec{a}_A\) from its normal and tangential components:
\(\vec{a}_A = \vec{a}_A^n + \vec{a}_A^t = \vec{\omega}_2 \times (\vec{\omega}_2 \times \vec{r}_{O2A}) + \vec{\alpha}_2 \times \vec{r}_{O2A}\)
aA = cross(w2, cross(w2, rO2A)) + cross(af2, rO2A);
Now, analyzing point B as part of link 3, we have:
\(\vec{a}_{B3} = \vec{a}_A + \vec{a}_{B/A}\)
which, by decomposing, gives:
\(\vec{a}_{B3} = \vec{a}_A + \vec{a}_{B/A}^n + \vec{a}_{B/A}^t\)
where the acceleration of A is known, and we can express the components of the relative acceleration from the available information:
For \(\vec{a}_{B/A}^n\), everything is known. Therefore: \(\vec{a}_{B/A}^n = \vec{\omega}_3 \times (\vec{\omega}_3 \times \vec{r}_{AB})\)
aB_An = cross(w3, cross(w3, rAB));
For \(\vec{a}_{B/A}^t\), we can operate and express it in terms of the unknown \(\vec{\alpha}_3\), of which we only know its direction: \(\vec{a}_{B/A}^t = \vec{\alpha}_3 \times \vec{r}_{AB}\)
syms af3k real
af3 = [0 0 af3k];
aB_At = cross(af3, rAB);
Which leaves us with:
aB3 = aA + aB_An + aB_At;
On the other hand, if we consider point B as part of link 4, we have:
\(\vec{a}_{B4} = a_B\hat{i}\)
syms aBi real
aB4 = [aBi 0 0];
Finally, if we equate both expressions, we have:
sol_ac1 = solve(aB3 == aB4, af3k, aBi);
af3k = double(subs(sol_ac1.af3k));
aBi = double(subs(sol_ac1.aBi));
fprintf('af3k=%0.3f aBi=%0.3f\n', af3k, aBi)
af3k=0.127 aBi=-0.277
Acceleration Cinema#
The acceleration cinema for this example is not provided, but it can be created using the same principles demonstrated in previous examples.
Example 2.13 - Acceleration Analysis of a Quick-Return Mechanism#
The figure shows a 4-bar quick-return mechanism, in which the slider represents the expansion movement of a cylinder (e.g., a truck’s hydraulic cylinder) at a constant velocity of \(0.1\) m/s. At the instant when the crank forms an angle \(\theta_2 = 20^{\circ}\) with the horizontal, calculate the acceleration of point B and the angular accelerations of links 2 and 4.

Data:
Link lengths, in meters: \(\overline{O_2 A} = 1.0;\, \overline{O_4 B} = 3.0;\, \overline{O_2 O_4} = 3.0\). Angle of link 4 with the horizontal (from position analysis): \(\theta_4 = 170.56^{\circ}\) and position of slider A relative to \(O_4\): \(d = \overline{O_4 A} = 2.089\) m. Angular velocities (from velocity analysis): \(\vec{\omega}_2 = 0.203\hat{k}\) rad/s; \(\vec{\omega}_4 = -0.085\hat{k}\) rad/s.
Resolution#
The procedure for calculating the mechanism’s accelerations is similar to that for velocities, taking into account that this time the Coriolis acceleration is involved:
\(\vec{a}_{A_2} = \vec{a}_{A_4} + \vec{a}_{A_2/A_4} + \vec{a}_{Cor}\)
where each term can be expressed as:
\(\vec{a}_{A_2} = \vec{\omega}_2 \times (\vec{\omega}_2 \times \vec{r}_{O2A}) + \vec{\alpha}_2 \times \vec{r}_{O2A}\)
syms af2k real
af2 = [0 0 af2k];
aA2 = cross(w2, cross(w2, rO2A)) + cross(af2, rO2A);
\(\vec{a}_{A_4} = \vec{\omega}_4 \times (\vec{\omega}_4 \times \vec{r}_{O4A}) + \vec{\alpha}_4 \times \vec{r}_{O4A}\)
syms af4k real
af4 = [0 0 af4k];
aA4 = cross(w4, cross(w4, rO4A)) + cross(af4, rO4A);
\(\vec{a}_{A_2/A_4} = 0\) (constant expansion velocity)
aA2_A4 = [0 0 0];
\(\vec{a}_{Cor} = 2\vec{\omega}_4 \times \vec{v}_{A2/A4}\)
aCor = 2 * cross(w4, vA2_A4);
Now we can solve the relative acceleration equation:
eq2 = aA2 == aA4 + aA2_A4 + aCor;
sol_a1 = solve(eq2, af2k, af4k);
af2k = double(subs(sol_a1.af2k));
af4k = double(subs(sol_a1.af4k));
fprintf('af2k=%0.3f af4k=%0.3f\n', af2k, af4k)
af2k=-0.104 af4k=0.061
Finally, we calculate the acceleration of point B now that we know \(\vec{\alpha}_4\):
aB = double(subs(cross(w4, (cross(w4, rO4B))) + cross(af4, rO4B)));
fprintf('aBi=%0.3f aBj=%0.3f\n', aB(1), aB(2))
aBi=-0.009 aBj=-0.185
fprintf('|aB|=%0.3f\n', norm([aB(1) aB(2)]))
|aB|=0.185
Acceleration Cinema#
The acceleration cinema for this example is not provided, but it can be created using the same principles demonstrated in previous examples.