DOF solved problems

This page presents some examples of determining the number of d.o.f. in a mechanism using the Gruebler’s formula as seen in the former section.

Example 1

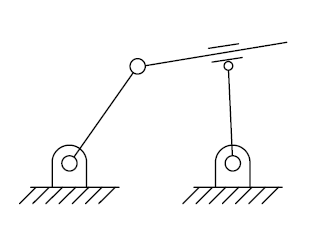
(Image credits: [AI14])

Solution

Two valid solutions:

\[n= 4, p_I=3, p_{II}=1 \rightarrow g=2\]

or

\[n= 5, p_I=5, p_{II}=0 \rightarrow g=2 \]

 

Example 2

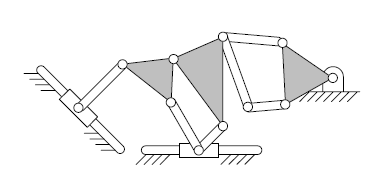
(Image credits: [AI14])

Solution

Two valid solutions:

\[ n= 12, p_I=15, p_{II}=0 \rightarrow g=3 \]

or

\[ n= 11, p_I=13, p_{II}=1 \rightarrow g=3 \]

 

Example 3

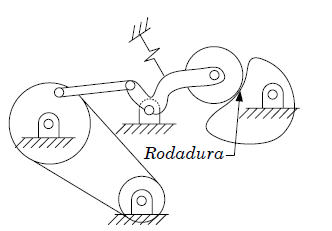
(Image credits: [AI14])

Solution

Do not count neither the disk at the bottom, nor the belt coupling. Grüebler fails with belts and gears, we must skip them.

\[ n= 6, p_I=7, p_{II}=0 \rightarrow g=1 \]

or (counting the cam as a type II joint instead):

\[ n= 5, p_I=5, p_{II}=1 \rightarrow g=1 \]

 

Example 4

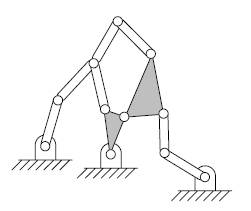
(Image credits: [AI14])

Solution

\[ n= 10, p_I=12, p_{II}=0 \rightarrow g=3 \]

 

Example 5

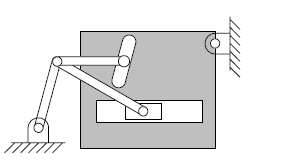
(Image credits: [AI14])

Solution

\[ n= 5, p_I=4, p_{II}=2 \rightarrow g=2 \]

or

\[ n= 7, p_I=8, p_{II}=0 \rightarrow g=2 \]

 

Example 6

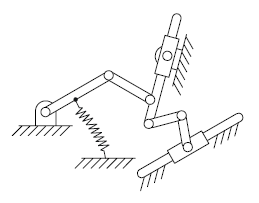
(Image credits: [AI14])

Solution

\[ n= 6, p_I=5, p_{II}=2 \rightarrow g=3 \]

or:

\[ n= 8, p_I=9, p_{II}=0 \rightarrow g=3 \]

 

Example 7

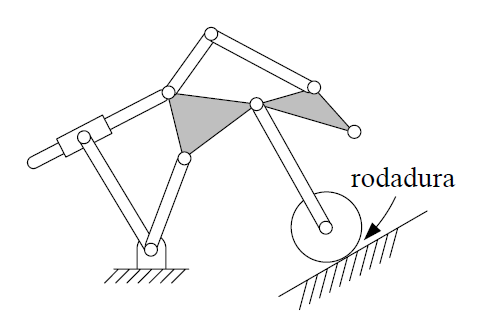
(Image credits: [AI14])

Solution

\[ n= 9, p_I=9, p_{II}=2 \rightarrow g=4 \]

or:

\[ n= 11, p_I=13, p_{II}=0 \rightarrow g=4 \]