Definitions#
Machines vs Mechanisms#
Machine
Set of bodies, put together such they have relative motion and transmit forces from one power source towards a place where work needs to be done
Mechanism
Set of bodies such that they can achieve some particular desired movement
Structure
Set of bodies without relative motion between them, capable of transmitting forces and resist loads
Blurry limits: machine vs mechanism#
Machine: More stress on transmitting power. Remember: \(P=F \cdot V\), \(P=\tau \cdot \omega\)
Mechanism: The focus is more on how movement is transformed.
Parts of a mechanism#
A mechanism comprises:
Also named elements, or links or bars. These are rigid bodies.
Elements that permit relative motion between two bodies.
| Systematic analysis of machines due to Franz Reuleaux (1829-1905). |
|
Parts of a link#
“A piece of a machine of mechanism with a relative motion to any other”
“Indivisible piece of an element or mechanism”

Kinematic pairs (Joints)#
Between two contiguous bodies.
In permanent contact.
With relative motion between them. The degree of the joint is the number of d.o.f. allowed by the joint.
Kinematic chain#
Kinematic chain:
“Set of bodies put together with joints, such that they have relative motion”
Mechanism:
“A kinematic chain, with one fixed element (ground)”
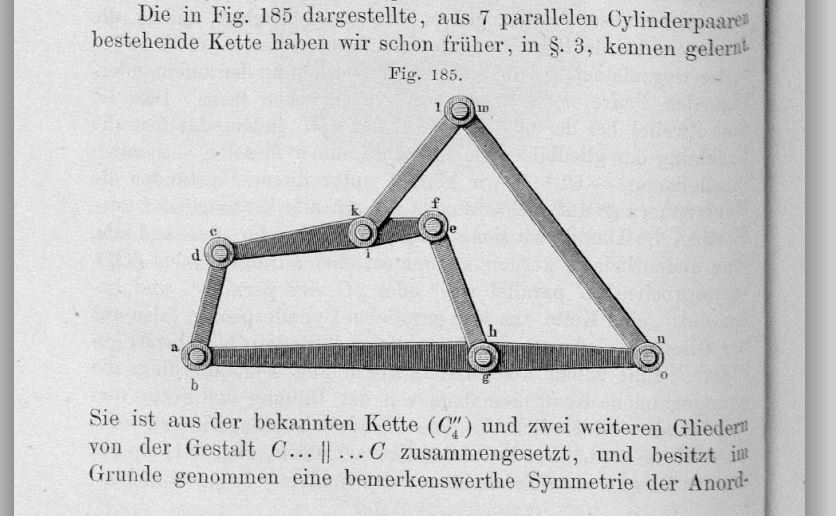
Abstract and topological analysis of mechanisms#
Franz Reuleaux proposed that it is enough to study the abstract kinematic chain of a mechanism to analyze its kinematic behavior.
In his 1886 book he invented an abstract notation to describe complex kinematic chains:
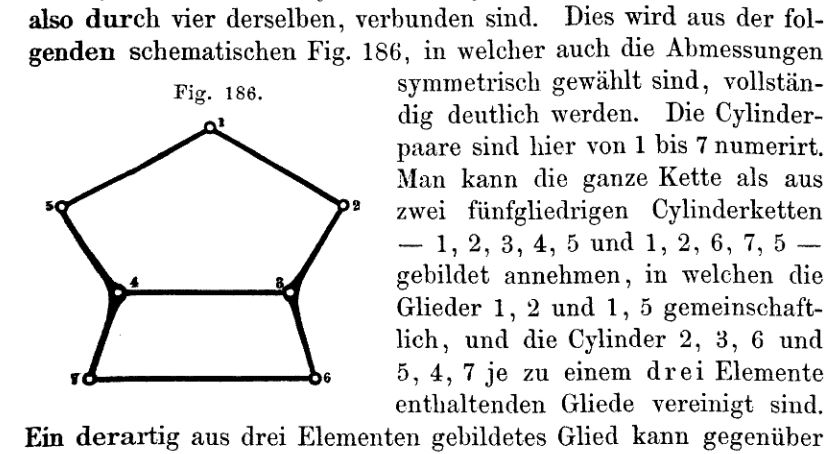
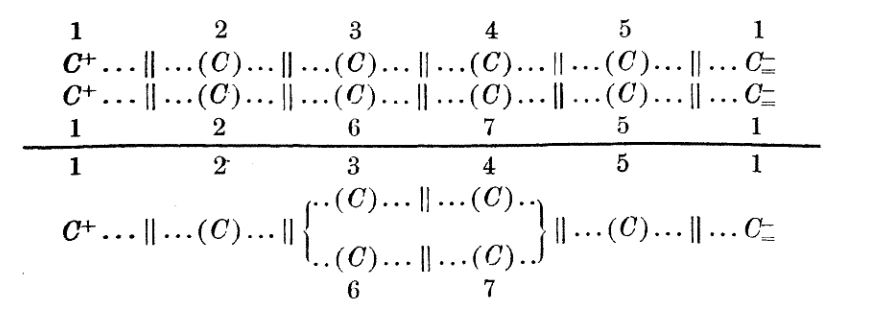
In some modern computer-based numerical methods, determining the graph corresponding to the mechanism chain remains being a key step.
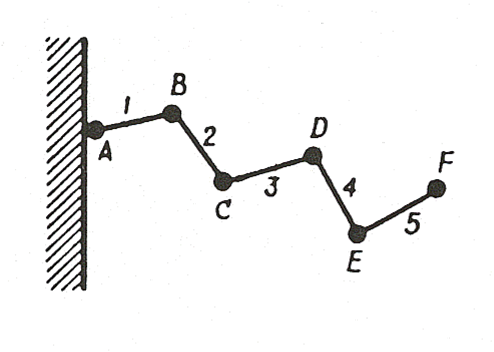
Open and closed kinematic chains#
It depends on the existence of loops in the kinematic chain topology.
Mobility and degrees of freedom#
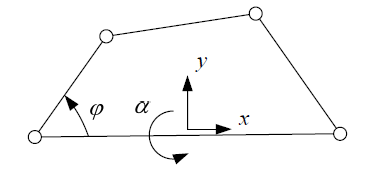
Mobility (\(M\)): number of parameters that must be specified to complete define its position.
Degrees of freedom (\(G\)): Idem. Due to the ground element, we have \(G = M - 3\) (for planar mechanisms).
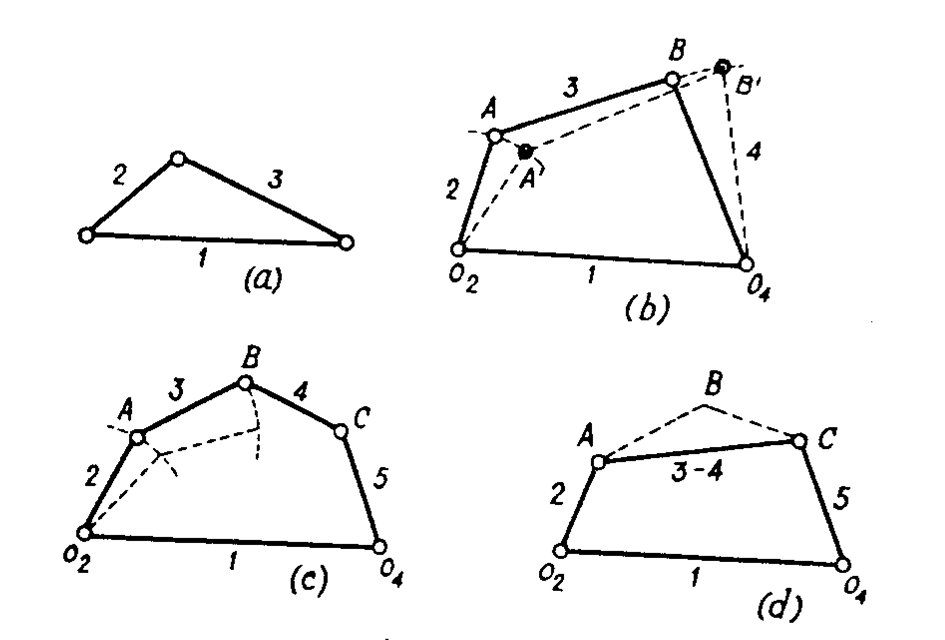
Equivalent mechanisms#
A mechanism, in a particular position, is kinematically equivalent to another one if it undergoes the same velocities and accelerations.

Inversions of a mechanism#
Swapping the role of two elements
If we focus on the role of “ground” (fixed element), then there exist \(N-1\) inversions.