Determining the d.o.f. count#
Grüebler formula for planar mechanisms#
It is a systematic method to find out the number of d.o.f. of a mechanism.
With:
\(G\): Overall d.o.f. (The result we are looking for!)
\(N\): Number of links/bodies, including the ground body.
\(p_{I},p_{II}\): Number of I and II-degrees joints.
Formula discussion:
Each planar body => 3N d.o.f.
We always have a “ground” body. Hence the ``-1’’.
Each I or II-degrees joint subtracts 2 or 1 d.o.f., respectively.
Practical application of the formula#
Number all links: Ground is #1, etc.
Identify kinematic links: Tell grade I from grade II.
Apply the formula: \(G=3(N-1) -2 p_{I} - p_{II}\)
Numbering options#
It is common to find more than one way to number links and joints, but they will eventually be equivalent. For example:
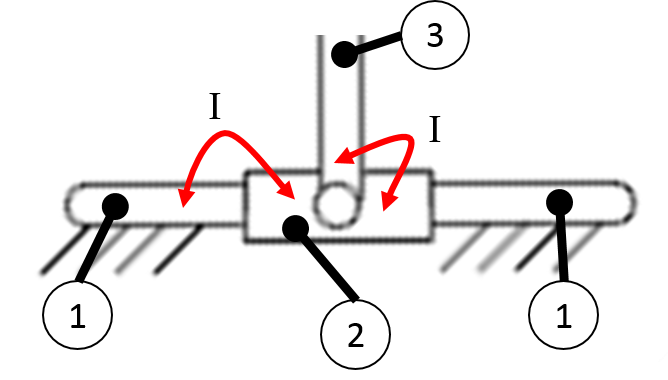
Slider block as a link and two type I joints.
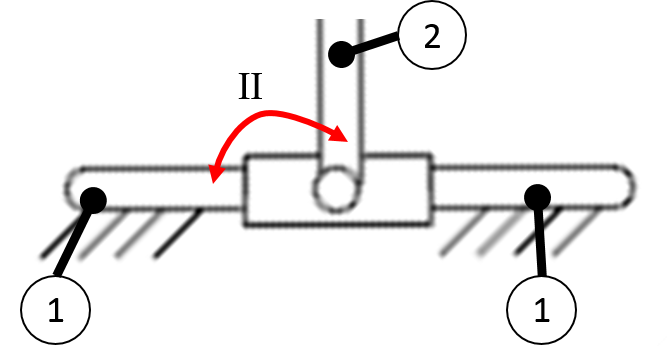
Do not count the block, but do count one type II joint.
Joints with more than two links#
When more than two bars arrive at one single joint, we have to analyze in which way they move with respect to each other. Example:
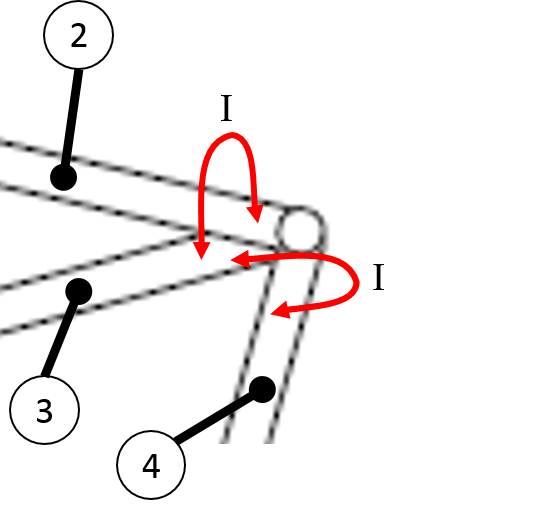
Articulation with three bars
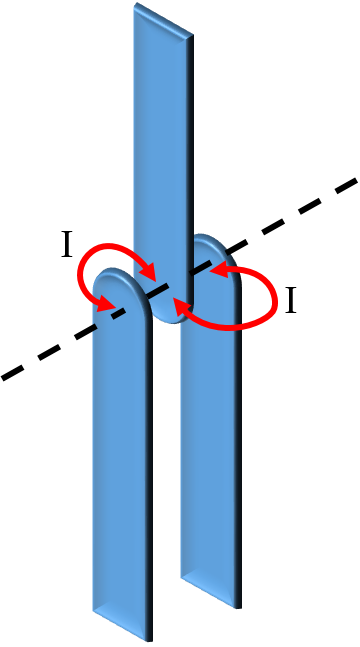
There exist two revolute joints (grade I).
Numerical methods criterion#
When using multibody formulations for machine and mechanism analysis, there exists a more advanced alternative to Gruebler’s method:
Based on the Jacobian matrix of the constraints
It works for both, 2D and 3D mechanisms
It detects singular configurations (Gruebler fails!)
This method will not be studied in the present introductory course.