Four bar linkage

One of the most common mechanisms:

• Four rigid bodies: #1 (ground), and three moving bars #2, #3, and #4.

• Two moving points: A and B.

• Two fixed points: \(O_2\) and \(O_4\).

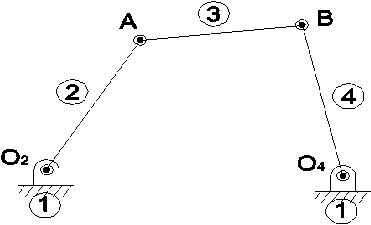
It features one degree of freedom: moving one bar fully determines the position of all other bars. The same applies to velocities and accelerations: fixing the velocity or acceleration of one “input” bar, we can compute the corresponding values for the whole mechanism.

Bar names

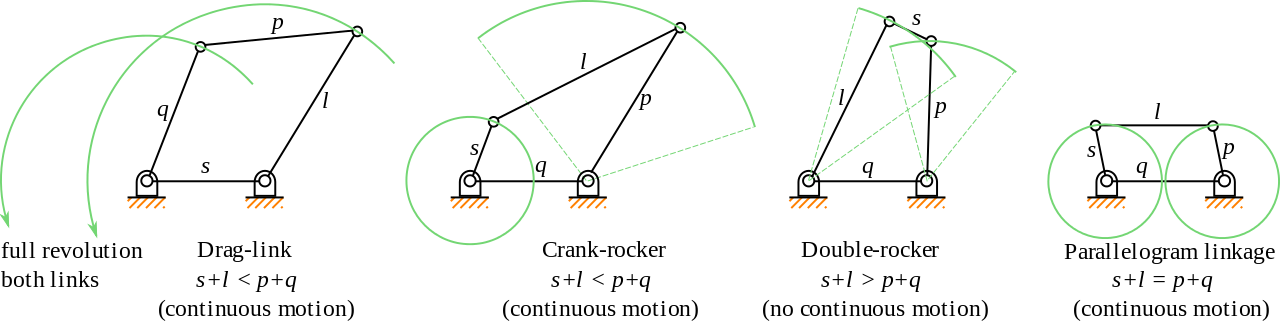
• Crank: If it touches the ground and can undergo complete revolutions. We may have 0, 1, or 2 cranks in a four-bar mechanism.

• Rocker: If it touches the ground and can only go back and forth. We may have 0, 1, or 2 rockers.

• Connecting rod: the bar that is not touching the ground.

Grashof’s formula

For one or two of the bars to be cranks, the sum of the longest (L) and shortest (S) bars should not be greater than the sum of the other two.

\[\begin{equation*} S + L \leq P + Q \end{equation*}\]

Example of a case with a double crank:

To find out more details on the kind of motion, there is a criterion to find out whether there is one or two cranks. First, we name bar lengths according to their role:

• \(a\): Input bar (left)

• \(b\): Output bar (right)

• \(g\): Ground bar

• \(h\): Connecting rod (top)

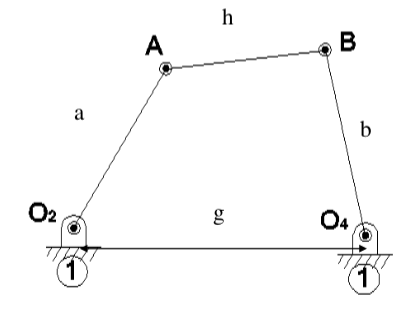
Then, we may have 8 different situations (bar names are shown for both, the picture above, and the interactive demo later on):

Test variables:

\[\begin{eqnarray*} T_1=g+h-a-b = r_1 + r_3 - r_2 - r_4 \\ T_2=b+g-a-h = r_4 + r_1 - r_2 - r_3 \\ T_3=b+h-a-g = r_4 + r_3 - r_2 - r_1 \\ \end{eqnarray*}\]

Possible outcomes:

	Linkage type	\(T_1\)	\(T_2\)	\(T_3\)
1	Crank-rocker	+	+	+
2	Rocker-crank	+	-	-
3	Double-crank	-	-	+
4	Double-rocker	-	+	-
5	Double-rocker	-	-	-
6	Double-rocker	+	+	-
7	Double-rocker	+	-	+
8	Double-rocker	-	+	+

Try it yourself!

Change the bar lengths in this interactive demo (source) to verify the Grashof’s formula:

Some tips:

• Drag the slider \(\theta_2\)

• The lengths \(a\), \(b\), \(g\), and \(h\) above are named \(r_2\), \(r_4\), \(r_1\), and \(r_3\) in the Geogebra model, respectively.

• Example of double-crank: \((r_1,r_2,r_3,r_4)=(5,7,8,9)\). \(T_1=5+8-7-9=-\), \(T_2=9+5-7-8=-\), \(T_3=9+8-5-7=+\) (--+).