Particle dynamics#
Linear momentum#
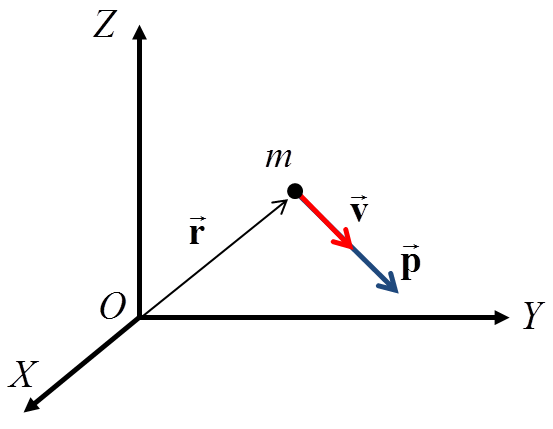
The linear momentum of a particle is a vector magnitude given in an inertial reference frame:
\[\mathbf{p} = m \mathbf{v}\]
Second Newton’s Law
\[ \mathbf{F} = \dot{ \mathbf{p} } \]
Principle of momentum conservation
\[ \mathbf{F} = 0 \rightarrow \mathbf{p} = constant \]
Angular momentum of a particle#
Definition
The angular momentum of a particle with respect to a point (\(O\)) is:
\[ \mathbf{L} = \mathbf{r} \times \mathbf{p} \]
Rate of change of the angular momentum
\[ \mathbf{M}_{O} = \frac{d}{dt}\left( \mathbf{r} \times \dot{\mathbf{p}} \right) = \dot{\mathbf{L}} \]
Principle of angular momentum conservation
\[ \mathbf{M} = 0 \rightarrow \mathbf{L} = constant\]
Equations of motion for a particle#
For a single particle, we have a system of differential equations:
\[\begin{split}
\begin{eqnarray*}
\mathbf{F} &=& \dot{ \mathbf{p} } \quad\quad \text{Newton (1643-1727)} \\
\mathbf{M}_{O} &=& \dot{\mathbf{L}} \quad\quad \text{Euler (1707-1783)}
\end{eqnarray*}
\end{split}\]
Note these amounts to six equations for 3D point-like particles. However, they are redundant, and solving just three of them is enough.
Picking the first subset (Newton’s second law): Since \(\dot{ \mathbf{p} } = \frac{d}{dt}( m \mathbf{v} ) = \frac{d}{dt}( m \dot{\mathbf{r}} ) = m \ddot{\mathbf{r}} \):
\[ m \ddot{\mathbf{r}} = \mathbf{F} \]
Which is a system of 3 ordinary differential equations (ODE):
\[\begin{split}
\begin{eqnarray*}
\ddot{x}(t) = \frac{1}{m} F_x(t) \\
\ddot{y}(t) = \frac{1}{m} F_y(t) \\
\ddot{z}(t) = \frac{1}{m} F_z(t)
\end{eqnarray*}
\end{split}\]
This ODE system can then be solved analytically (ideal cases only), or, more realistically, using numerical integrators: Euler, Trapezoidal, etc.