Introduction to Kinematic Analysis#
Kinematic analysis is the study of the geometry of motion. Its objective is to determine the position, velocity, and acceleration of all components of a mechanism to understand how they move, without considering the forces that cause this motion. This analysis is the fundamental pillar on which dynamic analysis is built, which does consider forces and inertias, making it an indispensable step in the design of any machine.
The process is approached sequentially and orderly:
Position Analysis: Determines the location and orientation of each link at a given instant.
Velocity Analysis: Calculates the linear and angular velocities of the links. It requires prior knowledge of the position.
Acceleration Analysis: Calculates the linear and angular accelerations. It requires prior knowledge of position and velocity.
1. Fundamentals: Vectors in Mechanism Analysis#
Planar mechanisms are modeled as a set of vectors in the XY plane. Vector representation allows us to mathematically describe the length and orientation of each link.
A position vector \(\vec{R}\) representing a link of length \(L\) and angle \(\theta\) can be expressed in two ways:
Cartesian Form: \(\vec{R} = R_x \hat{i} + R_y \hat{j} = (L \cos\theta) \hat{i} + (L \sin\theta) \hat{j}\)
Polar (or Complex) Form: \(\vec{R} = L e^{j\theta} = L(\cos\theta + j\sin\theta)\)
Complex notation is particularly powerful, as differentiation with respect to time to obtain velocity and acceleration is greatly simplified.
Vector Derivatives: Velocity and Acceleration#
Consider a point P whose position is given by the vector \(\vec{R}_P\), which rotates with an angular velocity \(\vec{\omega}\) and an angular acceleration \(\vec{\alpha}\) (in the plane, \(\vec{\omega} = \omega \hat{k}\) and \(\vec{\alpha} = \alpha \hat{k}\)).
Velocity#
The velocity of point P is the first time derivative of its position: \( \vec{v}_P = \frac{d\vec{R}_P}{dt} = \frac{d}{dt}(L e^{j\theta}) = L(j \dot{\theta})e^{j\theta} = j \omega L e^{j\theta} = j \omega \vec{R}_P \) In cross product vector notation: \( \vec{v}_P = \vec{\omega} \times \vec{R}_P \) The operator \(j\) (or the cross product with \(\vec{\omega}\)) rotates the original position vector \(\vec{R}_P\) by 90° in the direction of \(\omega\). Therefore, the linear velocity of a point in pure rotation is always perpendicular to its radius of rotation.
Acceleration#
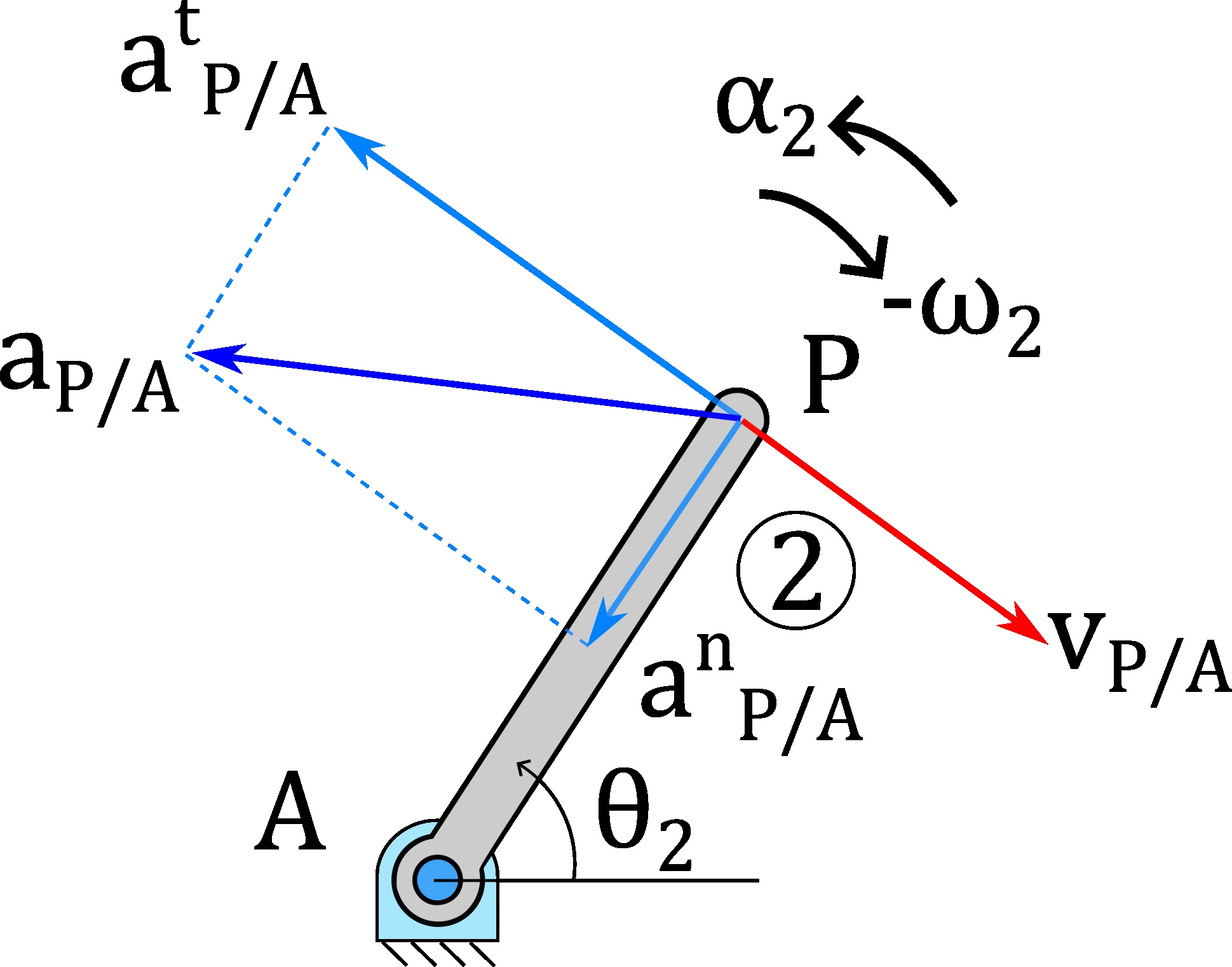
The acceleration is the second time derivative of the position: \( \vec{a}_P = \frac{d\vec{v}_P}{dt} = \frac{d}{dt}(j \omega \vec{R}_P) = j \dot{\omega} \vec{R}_P + j \omega \dot{\vec{R}}_P = j \alpha \vec{R}_P + j \omega (j \omega \vec{R}_P) = j \alpha \vec{R}_P - \omega^2 \vec{R}_P \) This equation reveals two fundamental components of acceleration:
Tangential Acceleration (\(\vec{a}_P^t\)): This is the term \(\vec{a}_P^t = j \alpha \vec{R}_P = \vec{\alpha} \times \vec{R}_P\).
It is due to the change in the magnitude of the velocity.
Its direction is perpendicular to the position vector \(\vec{R}_P\).
Its magnitude is \(a^t = |\alpha| L\).
Normal Acceleration (\(\vec{a}_P^n\)): This is the term \(\vec{a}_P^n = -\omega^2 \vec{R}_P = \vec{\omega} \times (\vec{\omega} \times \vec{R}_P)\).
It is due to the change in the direction of the velocity vector.
Its direction is parallel to the position vector \(\vec{R}_P\), but in the opposite direction (always pointing towards the center of rotation).
Its magnitude is \(a^n = \omega^2 L\).
The total acceleration is the vector sum of both: \(\vec{a}_P = \vec{a}_P^t + \vec{a}_P^n\).